Question
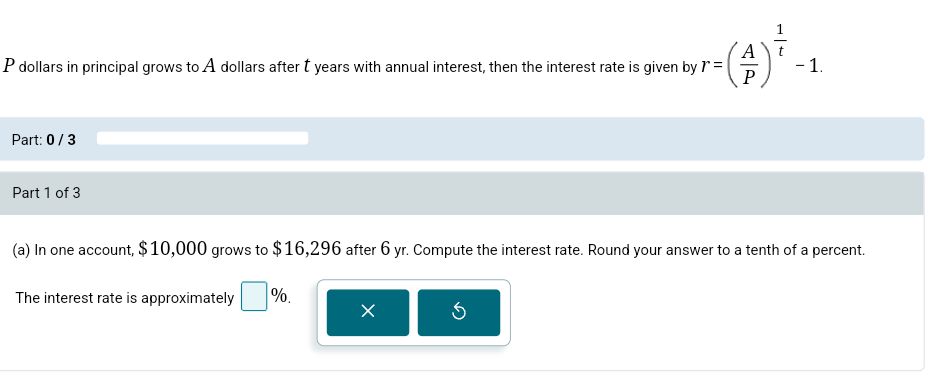
(a) In one account,
(a) In one account,
Ask by May Paul. in the United States
Dec 02,2024
Upstudy AI Solution
Tutor-Verified Answer
Answer
8.5%
Solution
Sign in to Unlock Answers for Free! ![]()
A Learning Platform Trusted by Millions of Real Students and Teachers.
 Unlock
Unlock Answered by UpStudy AI and reviewed by a Professional Tutor
Like
Mind Expander
To find the interest rate
Now applying the formula:
Calculating
Next, we calculate
Using a calculator, we find:
Now, substituting back into the formula for
Convert this decimal into a percentage:
Rounded to a tenth of a percent, the interest rate is approximately


