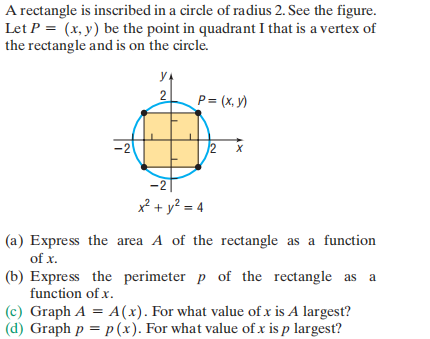
A rectangle is inscribed in a circle of radius \( 2 \) . See the figure. Let \( P = ( x , y ) \) be the point in quadrant I that is a vertex of the rectangle and is on the circle. (a) Express the area \( A \) of the rectangle as a function of \( x \) . (b) Express the perimeter \( p \) of the rectangle as a function of \( x \) . (c) Graph \( A = A ( x ) \) . For what value of \( x \) is \( A \) largest? (d) Graph \( p = p ( x ) \) . For what value of \( x \) is \( p \) largest?
Real Tutor Solution
Quick Answer
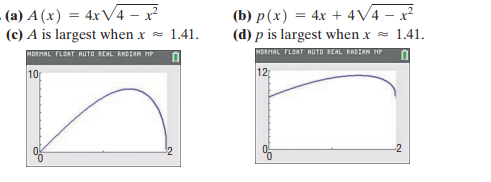
\(\left. \begin{array} { l l } { \text { (a) } A ( x ) = 4 x \sqrt { 4 - x ^ { 2 } } } & { \text { (b) } p ( x ) = 4 x + 4 \sqrt { 4 - x ^ { 2 } } } \\ { \text { (c) } A \text { is largest when } x \approx 1.41 . } & { \text { (d) } p \text { is largest when } x \approx 1.41 } \end{array} \right.\)
Enter your question here…