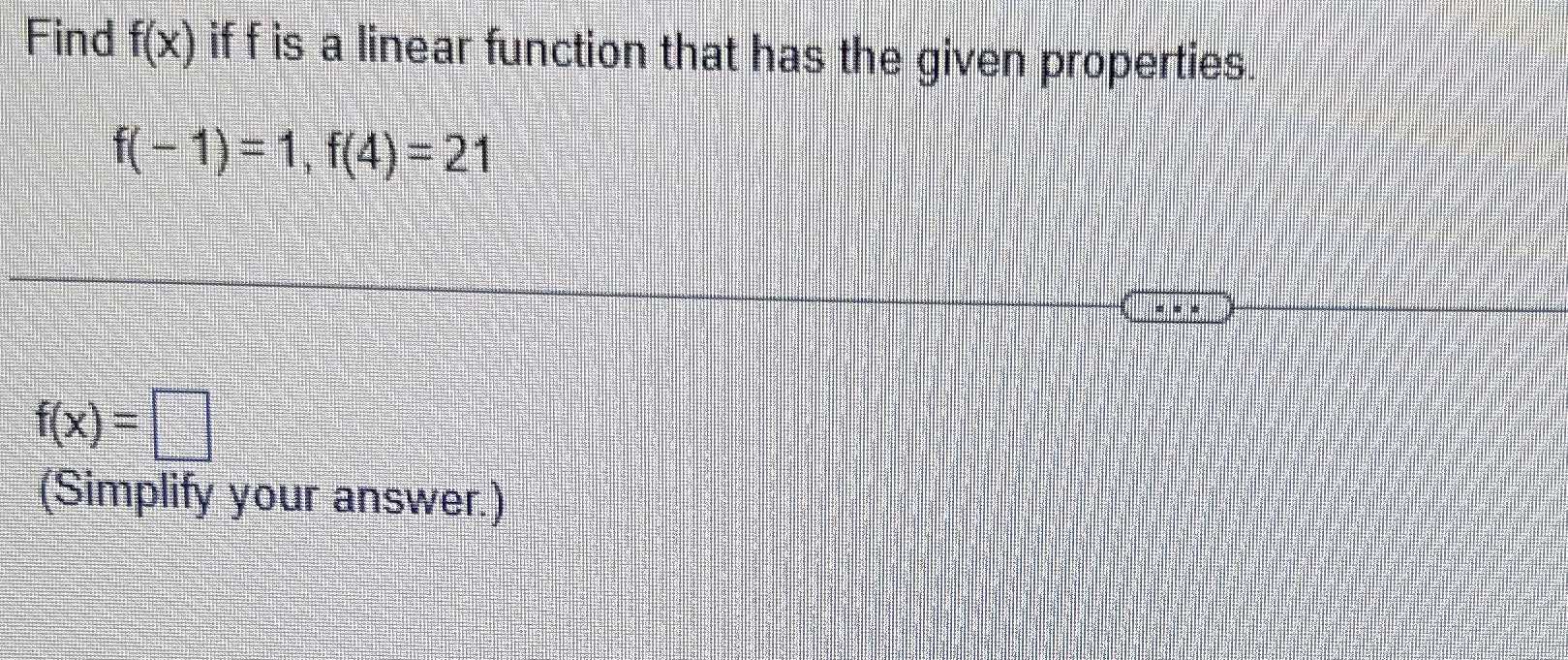
Find \( f ( x ) \) if \( f \) is a linear function that has the given properties. \( f ( - 1 ) = 1 , f ( 4 ) = 21 \) \( f ( x ) = \square \) (Simplify your answer.)
Real Tutor Solution
Quick Answer
Your input: find the equation of a line given two points \( P = ( - 1,1 ) \) and \( Q = ( 4,21 ) \)
The slope of a line passing through the two points \( P = ( x _ { 1 } , y _ { 1 } ) \) and \( Q = ( x _ { 2 } , y _ { 2 } ) \) is given by \( m = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \)
We have that \( x _ { 1 } = - 1 , y _ { 1 } = 1 , x _ { 2 } = 4 , y _ { 2 } = 21 \)
Plug the given values into the formula for slope: \( m = \frac { ( 21 ) - ( 1 ) } { ( 4 ) - ( - 1 ) } = \frac { 20 } { 5 } = 4\)
Now, the \( y \) -intercept is \( b = y _ { 1 } - m \cdot x _ { 1 } \) (or \( b = y _ { 2 } - m \cdot x _ { 2 } \) , the result is the same).
\( b = 1 - ( 4 ) \cdot ( - 1 ) = 5\)
Finally, the equation of the line can be written in the form \( y = m x + b \) .
\( y = 4 x + 5 \) .
The slope of the line is \( m = 4 \)
The equation of the line in the slope-intercept form is \( y = 4 x + 5 \) .
The equation of the line in the point-slope form is \( y - 1 = 4 ( x + 1 ) \) .
The equation of the line in the point-slope form is \( y - 21 = 4 ( x - 4 ) \) .
The general equation of the line is \( 4 x - y + 5 = 0 \) .
Enter your question here…