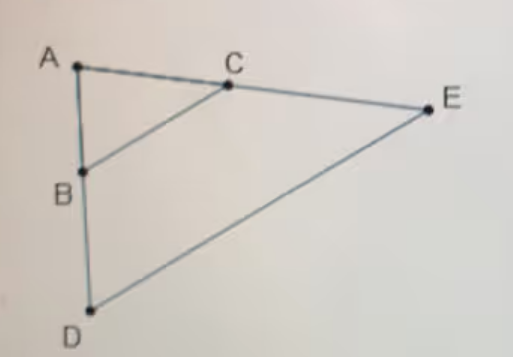
To prove that Delta AED Delta ACB by SAS, Jose shows that AE/AC = AD/ABJose also has to state that∠ A≌ ∠ A∠ A≌ ∠ D∠ A≌ ∠ ACB∠ A≌ ∠ ABC

To prove that triangles \(\Delta AED\) and \(\Delta ACB\) are similar by the Side-Angle-Side (SAS) similarity criterion, Jose needs to show that the ratios of corresponding sides are equal and that the included angle is congruent.
Jose has already shown that \(\frac { AE} { AC} = \frac { AD} { AB} \).
Now, for the angle, he must state that the angle included between these sides in both triangles is congruent. In this case, the included angle is \(\angle A\) in both triangles.
Thus, the correct statement is:
\[\angle A \equiv \angle A\]
This demonstrates that the included angle is the same in both triangles, satisfying the angle condition for SAS similarity.

Supplemental Knowledge

Geometry relies heavily on triangle congruence as an essential concept. According to the SAS (Side-Angle-Side) criteria, triangles that meet this condition have identical dimensions but differing orientation. If two sides and an included angle from any triangle meet these criteria then these triangles can be considered congruent; which implies having similar shapes, sizes, but possibly differing orientation.
To understand this better, consider two triangles \(\Delta PQR\) and \(\Delta XYZ\). If \(PQ = XY\), \(QR = YZ\), and the angle between these sides in both triangles (\(\angle PQR = \angle XYZ\)), then by SAS, \(\Delta PQR \cong \Delta XYZ\).

From Concepts to Reality

Imagine you're an architect designing two identical triangular windows for a building, and must ensure they match in size and shape so they fit precisely into their respective spaces. By measuring two sides of each window frame along with their angles between them and applying SAS criteria to determine their congruency criterion to confirm both triangular frames are congruent - this ensures consistent designs while maintaining structural integrity when installing these windows.

Understanding geometric concepts like triangle congruence can significantly boost problem-solving skills across various fields such as architecture, engineering and even art. At UpStudy we offer many resources that will deepen your understanding of geometry and other mathematical topics - explore our live tutor question bank or leverage AI powered problem-solving services so that you can quickly master these topics with ease!
For those delving into geometry problems like Jose's, UpStudy's Geometry Calculator is an excellent tool to assist you in verifying your work and gaining further insights into geometric proofs. Embrace learning with UpStudy—your partner in academic excellence!