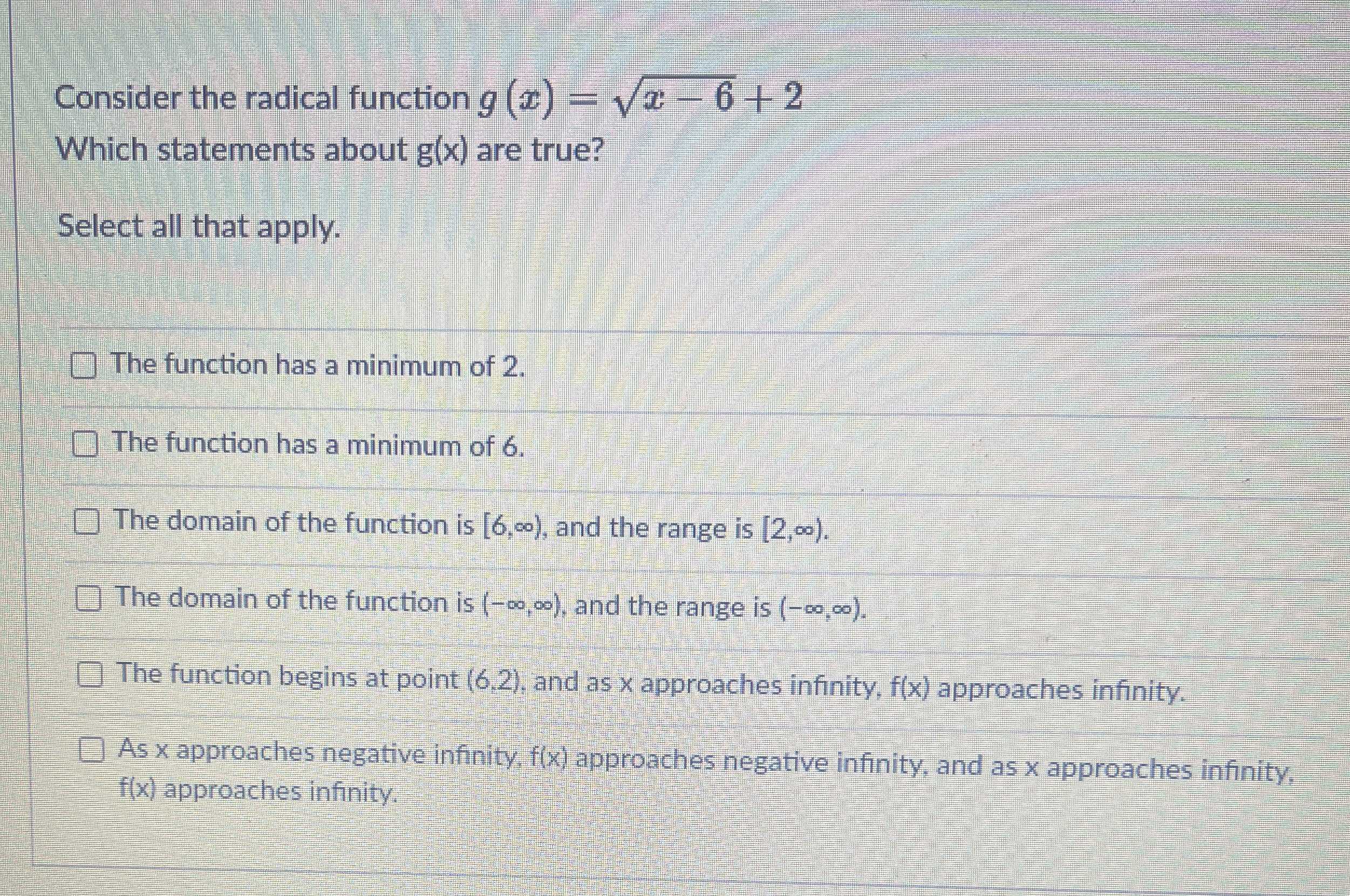
Consider the radical function \( g ( x ) = \sqrt { x - 6 } + 2 \) Which statements about \( g ( x ) \) are true? Select all that apply. \( \square \) The function has a minimum of \( 2 \) . \(\square \)The function has a minimum of \( 6 \) . \(\square \)The domain of the function is \( [ 6 , \infty ) \) , and the range is \( [ 2 , \infty ) \) . \(\square \)The domain of the function is \( ( - \infty , \infty ) \) , and the range is \( ( - \infty , \infty ) \) . \(\square \)The function begins at point \( ( 6,2 ) \) , and as \( x \) approaches infinity, \( f ( x ) \) approaches infinity. \(\square \)As \( x \) approaches negative infinity, \( f ( x ) \) approaches negative infinity, and as \( x \) approaches infinity, \(f( x) \)approaches infinity.
Real Tutor Solution
Quick Answer
b
Enter your question here…